Learning with errors
Learning with errors (LWE) is a problem in machine learning. A generalization of the parity learning problem, it has recently[1][2] been used to create public-key cryptosystems based on worst-case hardness of some lattice problems. The problem was introduced[1] by Oded Regev in 2005.
Given access to samples 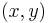 where
where 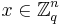 and
and 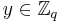 , with assurance that, for some fixed linear function
, with assurance that, for some fixed linear function 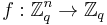
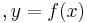 with high probability and deviates from it according to some known noise model, the algorithm must be able to recreate
with high probability and deviates from it according to some known noise model, the algorithm must be able to recreate  or some close approximation of it.
or some close approximation of it.
Contents |
Definition
Denote by 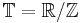 the additive group on reals modulo one. Denote by
the additive group on reals modulo one. Denote by 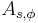 the distribution on
the distribution on 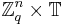 obtained by choosing a vector
obtained by choosing a vector 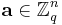 uniformly at random, choosing
uniformly at random, choosing  according to a probability distribution
according to a probability distribution  on
on 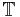 and outputting
and outputting 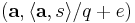 for some fixed vector
for some fixed vector 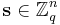 where the division is done in the field of reals, and the addition in
where the division is done in the field of reals, and the addition in 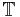 .
.
The learning with errors problem 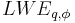 is to find
is to find 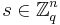 , given access to polynomially many samples of choice from
, given access to polynomially many samples of choice from 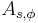 .
.
For every 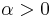 , denote by
, denote by 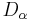 the one-dimensional Gaussian with density function
the one-dimensional Gaussian with density function 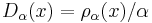 where
where 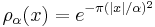 , and let
, and let 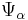 be the distribution on
be the distribution on 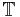 obtained by considering
obtained by considering 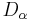 modulo one. The version of LWE considered in most of the results would be
modulo one. The version of LWE considered in most of the results would be 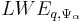
Decision version
The LWE problem described above is the search version of the problem. In the decision version, the goal is to distinguish between noisy inner products and uniformly random samples from 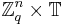 (practically, some discretized version of it). Regev[1] showed that the decision and search versions are equivalent when
(practically, some discretized version of it). Regev[1] showed that the decision and search versions are equivalent when  is a prime bounded by some polynomial in
is a prime bounded by some polynomial in  .
.
Solving decision assuming search
Intuitively, it is easy to see that if we have a procedure for the search problem, the decision version can be solved easily: just feed the input samples for the decision version to the procedure for the search problem, and check if the  returned by the search procedure can generate the input pairs modulo some noise.
returned by the search procedure can generate the input pairs modulo some noise.
Solving search assuming decision
For the other direction, suppose that we have a procedure for the decision problem, the search version can be solved as follows: Recover the  one co-ordinate at a time. Suppose we are guessing the first co-ordinate, and we are trying to test if
one co-ordinate at a time. Suppose we are guessing the first co-ordinate, and we are trying to test if 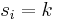 for a fixed
for a fixed 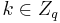 . Choose a number
. Choose a number 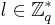 uniformly at random. Denote the given samples by
uniformly at random. Denote the given samples by 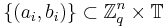 . Feed the transformed pairs
. Feed the transformed pairs  to the decision problem. It is easy to see that if the guess
to the decision problem. It is easy to see that if the guess  was correct, the transformation takes the distribution
was correct, the transformation takes the distribution 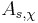 to itself, and otherwise takes it to the uniform distribution. Since we have a procedure for the decision version which distinguishes between these two types of distributions, and errs with very small probability, we can test if the guess
to itself, and otherwise takes it to the uniform distribution. Since we have a procedure for the decision version which distinguishes between these two types of distributions, and errs with very small probability, we can test if the guess  equals the first co-ordinate. Since
equals the first co-ordinate. Since  is a prime bounded by some polynomial in
is a prime bounded by some polynomial in  ,
,  can only take polynomially many values, and each co-ordinate can be efficiently guessed with high probability.
can only take polynomially many values, and each co-ordinate can be efficiently guessed with high probability.
Hardness results
Regev's result
For a n-dimensional lattice  , let smoothing parameter
, let smoothing parameter 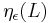 denote the smallest
denote the smallest  such that
such that 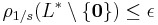 where
where 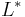 is the dual of
is the dual of  and
and 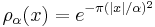 is extended to sets by summing over function values at each element in the set. Let
is extended to sets by summing over function values at each element in the set. Let 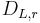 denote the discrete Gaussian distribution on
denote the discrete Gaussian distribution on  of width
of width  for a lattice
for a lattice  and real
and real 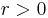 . The probability of each
. The probability of each 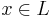 is proportional to
is proportional to 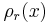 .
.
The discrete Gaussian sampling problem(DGS) is defined as follows: An instance of 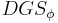 is given by an
is given by an  -dimensional lattice
-dimensional lattice  and a number
and a number 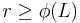 . The goal is to output a sample from
. The goal is to output a sample from 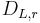 . Regev shows that there is a reduction from
. Regev shows that there is a reduction from 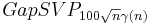 to
to 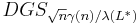 for any function
for any function  .
.
Regev then shows that there exists an efficient quantum algorithm for 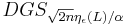 given access to an oracle for
given access to an oracle for 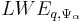 for integer
for integer  and
and 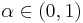 such that
such that 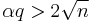 . This implies the hardness for
. This implies the hardness for 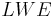 . Although the proof of this assertion works for any
. Although the proof of this assertion works for any  , for creating a cryptosystem, the
, for creating a cryptosystem, the  has to be polynomial in
has to be polynomial in  .
.
Peikert's result
Peikert proves[2] that there is a probabilistic polynomial time reduction from the  problem in the worst case to solving
problem in the worst case to solving 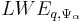 using
using 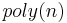 samples for parameters
samples for parameters 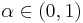 ,
, 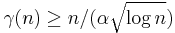 ,
, 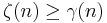 and
and 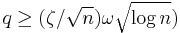 .
.
Use in Cryptography
The LWE problem serves as a versatile problem used in construction of several[1][2][3][4] cryptosystems. In 2005, Regev[1] showed that the decision version of LWE is hard assuming quantum hardness of the lattice problems  (for
(for  as above) and
as above) and 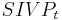 with t=Õ(n/
with t=Õ(n/ ). In 2009, Peikert[2] proved a similar result assuming only the classical hardness of the related problem
). In 2009, Peikert[2] proved a similar result assuming only the classical hardness of the related problem  . The disadvantage of Peikert's result is that it bases itself on a non-standard version of an easier (when compared to SIVP) problem GapSVP.
. The disadvantage of Peikert's result is that it bases itself on a non-standard version of an easier (when compared to SIVP) problem GapSVP.
Public-key cryptosystem
Regev[1] proposed a public-key cryptosystem based on the hardness of the LWE problem. The cryptosystem as well as the proof of security and correctness are completely classical. The system is characterized by 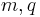 and a probability distribution
and a probability distribution 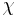 on
on 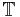 . The setting of the parameters used in proofs of correctness and security is
. The setting of the parameters used in proofs of correctness and security is
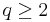 , a prime number between
, a prime number between 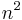 and
and 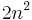 .
.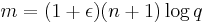 for an arbitrary constant
for an arbitrary constant 
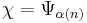 for
for 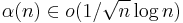
The cryptosystem is then defined by:
- Private Key: Private key is an
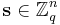 chosen uniformly at random.
chosen uniformly at random. - Public Key: Choose
 vectors
vectors 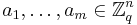 uniformly and independently. Choose error offsets
uniformly and independently. Choose error offsets 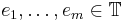 independently according to
independently according to 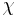 . The public key consists of
. The public key consists of 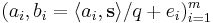
- Encryption: The encryption of a bit
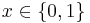 is done by choosing a random subset
is done by choosing a random subset  of
of ![[m]](/2012-wikipedia_en_all_nopic_01_2012/I/efc831aabf9ade051f781ccb54c2dcdb.png) and then defining
and then defining 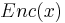 as
as 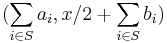
- Decryption: The decryption of
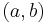 is
is 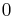 if
if 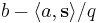 is closer to
is closer to 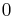 than to
than to 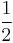 , and
, and 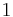 otherwise.
otherwise.
The proof of correctness follows from choice of parameters and some probability analysis. The proof of security is by reduction to the decision version of LWE: an algorithm for distinguishing between encryptions (with above parameters) of 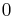 and
and 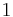 can be used to distinguish between
can be used to distinguish between 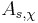 and the uniform distribution over
and the uniform distribution over 
CCA-secure cryptosystem
Peikert[2] proposed a system that is secure even against any chosen-ciphertext attack.
See also
References
- ^ a b c d e f Oded Regev, “On lattices, learning with errors, random linear codes, and cryptography,” in Proceedings of the thirty-seventh annual ACM symposium on Theory of computing (Baltimore, MD, USA: ACM, 2005), 84-93, http://portal.acm.org/citation.cfm?id=1060590.1060603.
- ^ a b c d e Chris Peikert, “Public-key cryptosystems from the worst-case shortest vector problem: extended abstract,” in Proceedings of the 41st annual ACM symposium on Theory of computing (Bethesda, MD, USA: ACM, 2009), 333-342, http://portal.acm.org/citation.cfm?id=1536414.1536461.
- ^ Chris Peikert and Brent Waters, “Lossy trapdoor functions and their applications,” in Proceedings of the 40th annual ACM symposium on Theory of computing (Victoria, British Columbia, Canada: ACM, 2008), 187-196, http://portal.acm.org/citation.cfm?id=1374406.
- ^ Craig Gentry, Chris Peikert, and Vinod Vaikuntanathan, “Trapdoors for hard lattices and new cryptographic constructions,” in Proceedings of the 40th annual ACM symposium on Theory of computing (Victoria, British Columbia, Canada: ACM, 2008), 197-206, http://portal.acm.org/citation.cfm?id=1374407.